Time scale calculus Source: en.wikipedia.org/wiki/Time_scale_calculus

In mathematics, time-scale calculus is a unification of the theory of difference equations with that of differential equations, unifying integral and differential calculus with the calculus of finite differences, offering a formalism for studying hybrid systems. It has applications in any field that requires simultaneous modelling of discrete and continuous data. It gives a new definition of a derivative such that if one differentiates a function defined on the real numbers then the definition is equivalent to standard differentiation, but if one uses a function defined on the integers then it is equivalent to the forward difference operator.

Time-scale calculus was introduced in 1988 by the German mathematician Stefan Hilger.^[1] However, similar ideas have been used before and go back at least to the introduction of the Riemann–Stieltjes integral, which unifies sums and integrals.

Many results concerning differential equations carry over quite easily to corresponding results for difference equations, while other results seem to be completely different from their continuous counterparts.^[2] The study of dynamic equations on time scales reveals such discrepancies, and helps avoid proving results twice—once for differential equations and once again for difference equations. The general idea is to prove a result for a dynamic equation where the domain of the unknown function is a so-called time scale (also known as a time-set), which may be an arbitrary closed subset of the reals. In this way, results apply not only to the set of real numbers or set of integers but to more general time scales such as a Cantor set.

The three most popular examples of calculus on time scales are differential calculus, difference calculus, and quantum calculus. Dynamic equations on a time scale have a potential for applications such as in population dynamics. For example, they can model insect populations that evolve continuously while in season, die out in winter while their eggs are incubating or dormant, and then hatch in a new season, giving rise to a non-overlapping population.

A time scale (or measure chain) is a closed subset of the real line ${\displaystyle \mathbb {R} }$. The common notation for a general time scale is ${\displaystyle \mathbb {T} }$.

The two most commonly encountered examples of time scales are the real numbers ${\displaystyle \mathbb {R} }$ and the discrete time scale ${\displaystyle h\mathbb {Z} }$.

A single point in a time scale is defined as:

${\displaystyle t:t\in \mathbb {T} }$

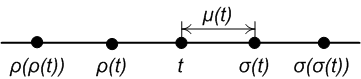
The forward jump and backward jump operators represent the closest point in the time scale on the right and left of a given point ${\displaystyle t}$, respectively. Formally:

${\displaystyle \sigma (t)=\inf\{s\in \mathbb {T} :s>t\}}$ (forward shift/jump operator)

${\displaystyle \rho (t)=\sup\{s\in \mathbb {T} :s<t\}}$ (backward shift/jump operator)

The graininess ${\displaystyle \mu }$ is the distance from a point to the closest point on the right and is given by:

${\displaystyle \mu (t)=\sigma (t)-t.}$

For a right-dense ${\displaystyle t}$, ${\displaystyle \sigma (t)=t}$ and ${\displaystyle \mu (t)=0}$.
For a left-dense ${\displaystyle t}$, ${\displaystyle \rho (t)=t.}$

For any ${\displaystyle t\in \mathbb {T} }$, ${\displaystyle t}$ is:

• left dense if ${\displaystyle \rho (t)=t}$
• right dense if ${\displaystyle \sigma (t)=t}$
• left scattered if ${\displaystyle \rho (t)<t}$
• right scattered if ${\displaystyle \sigma (t)>t}$
• dense if both left dense and right dense
• isolated if both left scattered and right scattered

As illustrated by the figure at right:

• Point ${\displaystyle t_{1}}$ is dense
• Point ${\displaystyle t_{2}}$ is left dense and right scattered
• Point ${\displaystyle t_{3}}$ is isolated
• Point ${\displaystyle t_{4}}$ is left scattered and right dense

Continuity of a time scale is redefined as equivalent to density. A time scale is said to be right-continuous at point ${\displaystyle t}$ if it is right dense at point ${\displaystyle t}$. Similarly, a time scale is said to be left-continuous at point ${\displaystyle t}$ if it is left dense at point ${\displaystyle t}$.

Take a function:

${\displaystyle f:\mathbb {T} \to \mathbb {R} ,}$

(where R could be any Banach space, but is set to the real line for simplicity).

Definition: The delta derivative (also Hilger derivative) ${\displaystyle f^{\Delta }(t)}$ exists if and only if:

For every ${\displaystyle \varepsilon >0}$ there exists a neighborhood ${\displaystyle U}$ of ${\displaystyle t}$ such that:

${\displaystyle \left|f(\sigma (t))-f(s)-f^{\Delta }(t)(\sigma (t)-s)\right|\leq \varepsilon \left|\sigma (t)-s\right|}$

for all ${\displaystyle s}$ in ${\displaystyle U}$.

Take ${\displaystyle \mathbb {T} =\mathbb {R} .}$ Then ${\displaystyle \sigma (t)=t}$, ${\displaystyle \mu (t)=0}$, ${\displaystyle f^{\Delta }=f'}$; is the derivative used in standard calculus. If ${\displaystyle \mathbb {T} =\mathbb {Z} }$ (the integers), ${\displaystyle \sigma (t)=t+1}$, ${\displaystyle \mu (t)=1}$, ${\displaystyle f^{\Delta }=\Delta f}$ is the forward difference operator used in difference equations.

The delta integral is defined as the antiderivative with respect to the delta derivative. If ${\displaystyle F(t)}$ has a continuous derivative ${\displaystyle f(t)=F^{\Delta }(t)}$ one sets

${\displaystyle \int _{r}^{s}f(t)\Delta (t)=F(s)-F(r).}$

A Laplace transform can be defined for functions on time scales, which uses the same table of transforms for any arbitrary time scale. This transform can be used to solve dynamic equations on time scales. If the time scale is the non-negative integers then the transform is equal^[2] to a modified Z-transform: $${\displaystyle {\mathcal {Z}}'\{x[z]\}={\frac {{\mathcal {Z}}\{x[z+1]\}}{z+1}}}$$

Partial differential equations and partial difference equations are unified as partial dynamic equations on time scales.^[3][4][5]

Multiple integration on time scales is treated in Bohner (2005).^[6]

Stochastic differential equations and stochastic difference equations can be generalized to stochastic dynamic equations on time scales.^[7]

Associated with every time scale is a natural measure^[8][9] defined via

${\displaystyle \mu ^{\Delta }(A)=\lambda (\rho ^{-1}(A)),}$

where ${\displaystyle \lambda }$ denotes Lebesgue measure and ${\displaystyle \rho }$ is the backward shift operator defined on ${\displaystyle \mathbb {R} }$. The delta integral turns out to be the usual Lebesgue–Stieltjes integral with respect to this measure

${\displaystyle \int _{r}^{s}f(t)\Delta t=\int _{[r,s)}f(t)d\mu ^{\Delta }(t)}$

and the delta derivative turns out to be the Radon–Nikodym derivative with respect to this measure^[10]

${\displaystyle f^{\Delta }(t)={\frac {df}{d\mu ^{\Delta }}}(t).}$

The Dirac delta and Kronecker delta are unified on time scales as the Hilger delta:^[11][12]

${\displaystyle \delta _{a}^{\mathbb {H} }(t)={\begin{cases}{\dfrac {1}{\mu (a)}},&t=a\\0,&t\neq a\end{cases}}}$

Fractional calculus on time scales is treated in Bastos, Mozyrska, and Torres.^[13]

• Analysis on fractals for dynamic equations on a Cantor set.
• Multiple-scale analysis
• Method of averaging
• Krylov–Bogoliubov averaging method

• Agarwal, Ravi; Bohner, Martin; O’Regan, Donal; Peterson, Allan (2002). "Dynamic equations on time scales: a survey". Journal of Computational and Applied Mathematics. 141 (1–2): 1–26. Bibcode:2002JCoAM.141....1A. doi:10.1016/S0377-0427(01)00432-0.
• Dynamic Equations on Time Scales Special issue of Journal of Computational and Applied Mathematics (2002)
• Dynamic Equations And Applications Special Issue of Advances in Difference Equations (2006)
• Dynamic Equations on Time Scales: Qualitative Analysis and Applications Special issue of Nonlinear Dynamics And Systems Theory (2009)

• The Baylor University Time Scales Group
• Timescalewiki.org