Talk:One way function Source: en.wikipedia.org/wiki/Talk:One_way_function
| This article is rated Start-class on Wikipedia's content assessment scale. It is of interest to the following WikiProjects: | ||||||||||||||||||||||||
| ||||||||||||||||||||||||
Clarification
[edit]I'd like some extra clarification introducing the topic. If a one-way-function means a function that is not reversible, it could be as simple as IsEven(int)->bool - you cannot recreate the input integer from it's output. Could someone please clarify how a one-way function differs from this? --198.160.96.7 (talk) 21:15, 11 April 2013 (UTC)
- It is actually reversible but prohibitively so. It's an important detail because it means it can be used in cryptography as opposed to basically destroying the input but zero-ing it. Utopiah (talk) 08:01, 18 May 2023 (UTC)
Bijection?
[edit]According to the definition of Oded Goldreich's book Foundations of Cryptography (Basic Tools), a one-way function does not need to be a bijection. And that does have some significant implication.
- That was just the question I was about to ask! Currently, we have: A cryptographic hash function is like a one way function except that it is not required to be bijective and has more stringent requirements for hardness of inversion. — Matt 09:58, 17 Nov 2004 (UTC)
- I'm the one who messed that up; sorry. I guess I thought the article was about one way permutations. Arvindn 03:06, 18 Nov 2004 (UTC)
There is currently no really good definition of what the desirable properties of a cryptographic hash are. They are basically expected to be maximally dull, but defining that is nearly impossible. ciphergoth 10:13, 2004 Nov 17 (UTC)
- I don't know about impossible; it may require care, have a look at Rogaway and Shrimpton's Cryptographic Hash-Function Basics: Definitions, Implications, and Separations for Preimage Resistance, Second-Preimage Resistance, and Collision Resistance [1] (though I'll freely admit that a bunch of this goes straight over my head at the moment!) — Matt 10:38, 17 Nov 2004 (UTC)
- Looking at that now. Note, for example, that it can't define collision resistance for a fixed hash function; it can only define it for a large family of hash functions, one of which is chosen at random. So we don't have a way to formally define an assertion such as "SHA-1 is collision resistant". For another example, I once exchanged quite a lot of email with John Kelsey and David Wagner trying to come up with a definition of what it would mean for a hash function to be good for entropy collection, and we basically drew a blank. See Ross Anderson's [The classification of hash functions] for some illustrations of the difficulties. ciphergoth 10:59, 2004 Nov 17 (UTC)
- Hmmm, yeah, the concepts do get quite slippery when you stare at them closely! — Matt 01:08, 18 Nov 2004 (UTC)
- But the Random Oracle Model is precisely such a definition (although many now consider it too idealistic to be achievable, even to an approximation). Unfortunately we don't yet have an article on the ROM. Arvindn 03:06, 18 Nov 2004 (UTC)
- We have Random oracle - but this should be re-titled "Random Oracle Model" since that's mostly what it's about. It's possible a separate article on random oracles would be appropriate, or a redirect to ROM would be appropriate. The ROM isn't such a definition - it's an idealization. See the Random oracle article for more - including how no hash function can reach the bar the ROM sets. I've just heard about some interesting new problems with the ROM, but I can't quite follow the papers, so I've asked David Molnar for help...
- I would be in favor of separate articles for "random oracle" and "random oracle model/methodology." The reason is that random oracles are of independent use in complexity theory, e.g. people are able to prove that complexity classes, relative to a random oracle, are the same/different with probability 1. (I don't know much more about this, though.) In contrast, in cryptography the random oracle model is a methodology for cryptographic design.
- This discussion really doesn't have anything to do with one-way functions, though. Even cryptographic hash functions are a far cry from one-way functions; we desire completely different things from them. --Chris Peikert 22:00, 18 Nov 2004 (UTC)
- (I've copied this thread to Talk:Random oracle). — Matt 10:17, 19 Nov 2004 (UTC)
I think it would be worth mentioning cryptographic hash functions here in some way. The first thing I thought when I read the definition was, "oh, so these are reminiscent of hash functions" (in the "preimage resistance"-y way); it's a natural question for a reader to ask, so it would be good to have a sentence explaining in what way they are similar, and in what way they are not. — Matt 10:25, 17 Nov 2004 (UTC)
- The only thing I can think to add is something like "A different, but similar concept in cryptography is that of the cryptographic hash function". ciphergoth 10:59, 2004 Nov 17 (UTC)
- That seems good enough to me. — Matt 01:08, 18 Nov 2004 (UTC)
Computing any preimage of (i.e., an element such that ), given only for some random , is not tractable (i.e. no probabilistic polynomial time algorithm exists).
Is this somewhat the same as computing x given f(x) is not tractable?
And why isn't, say, f(x) = 3 considered a one-way function? --Ihope127 21:16, 11 July 2005 (UTC)
- Actually it is. Not very usefull function though. -- Mike 15:40, 14 July 2005 (UTC)
- No, no it isn't, otherwise the question of their existence would be settled. Deco 19:22, 14 July 2005 (UTC)
- That is right. Succesfully inverting a function implies finding a solution to the function, not "the" solution. for f(x) =3, x could equal any number, thus the solution is trivial. 18.244.2.203 06:28, 28 February 2006 (UTC)
Removed question from the page
[edit]I removed this text from the page on the grounds that questions belong on talk pages:
- Question here for Bit Streams Cryptology: For mathematical equations in the lowest representation systems the binary systems of bits like "0" and "1", as like the equations with equal signs like "A = B", could we conclude that it is impossible to have one-way function because "B = A" as well and there is no imaginary number, no fractional number, no transcendental number, etc? What we have are only bit streams, hence it is an issues of Electricity Supply, CPU Computing Power, Memory Space, Data Transmission Speed, etc. The encrypted bit streams is in fact needing only a matching table to decode the hidden information. This is because certain blocks of bit streams are assigned to represent certain concepts.
I think they're saying something like "if the inputs and outputs are taken from finite sets, a suitably pre-compiled inverse lookup table, if available, could do the job in O(1) time." To which the answer is, I think, "yes, but first you not only have to have enough storage for the table, but you also have to pre-fill the table, unless you have an oracle that can present you with the entire table -- and filling the table is equivalent to brute force inversion by testing all the possible inputs, which is exponential-time in n". -- Karada 15:15, 14 July 2005 (UTC)
- Yes, this is totally bogus. Lots of "buzzwords" that have absolutely nothing to do with theoretical computer science. The definition of OWFs is against uniform inversion algorithms. That is, the same algorithm must be used to invert all sizes of inputs. You can hard-code a lookup table into the algorithm for any finite lengths of inputs, but not for all (infinitely many) input lengths.
Worst-case vs. cryptographic one-way functions
[edit]From the article:
- However, it has been shown that P≠UP (a subclass of NP) implies the existence of one-to-one one-way functions; see UP for more.
This is certainly confusing the notions of worst-case and cryptographic (weak/strong) one-way functions. A worst-case OWF is a function having no inverse computable in polynomial time. These exist iff P≠NP. Similarly, one-to-one worst-case OWFs exist iff P≠UP, poly-to-one worst-case iff P≠FewP, etc, etc... The proofs of these statements are all essentially the same.
Whether worst-case OWFs implies weak/strong OWFs is not known, and this is why the existence of cryptographic OWFs is a stronger assumption than P≠NP.
Anyway, the above statement surely needs to be removed, but should there also be a note about worst-case OWFs? They are still frequently used as tools in structural complexity. Blokhead 16:51, 13 October 2005 (UTC)
- I went ahead and removed that, if anyone thinks worst-case OWFs should also be included in the article, let me know and I can try to write something up..
Definition is incomprehensible to laymen
[edit]The notation and terminology used in the formal definition is just way beyond me, and 99% of our readership. Could we give examples of what a theoretical one-way function would do to an input, how any similar (existing and theoretical) categories of functions would differ in their output from the one-way function, and what the uses of the one-way function would be? For one of the most important unsolved problems in computer science, this page could be much clearer to the interested layman.
For specific points, two things came to mind when I heard the term "one-way function":
- For any even trivially lossy function, such as "replace the first bit of the input with 1", the input cannot be determined from the output with absolute certainty.
- Any function must be susceptible to brute force as a way to find inputs that match an output, even if brute force is not computationally feasible.
Both of these points are trivially true and thus probably irrelevant to this important question that I don't understand, but I would expect a fair number of people would think of things like that when they hear the term, so maybe they should be addressed. —Simetrical (talk • contribs) 00:22, 30 December 2005 (UTC)
- So if I understand correctly, you're asking for something more precise than the vague introduction statements but easier to understand than the formal definitions? Deco 01:40, 30 December 2005 (UTC)
- 1. Inverting doesn't require finding "the input", which is not unique. It only requires finding "any input", the hardness of which is not affected by making it lossy.
- 2. Sure, brute force will work - but brute force is always "hard".
- 3. For most cryptographic concepts it is plainly impossible to give definitions that are comprehensible to laymen. Hell, cryptographers ourselves spend hours staring at a definition before we fully understand them (and months or years coming up with them). Instead, one can give an explanation that is comprehensible to laymen followed by a definition proper. I agree the article is lacking in the first respect; you could go ahead and fix it yourself. Arvindn 02:59, 30 December 2005 (UTC)
Hmm. So this is basically what cryptographic hash functions are aiming for, just nobody's mathematically proven that any of them are actually one-way?
And what exactly (or inexactly) is meant by a function being "hard" to invert? It would mean, basically, that there's no way to do it except brute force? Or is the idea more complicated than that?
This is turning out to be simpler than I thought. I could write up a beginning once I get the basics here laid out. —Simetrical (talk • contribs) 11:02, 3 January 2006 (UTC)
- I have added small description of the most complex second condition. Is it better now? --Mike 20:51, 16 February 2006 (UTC)
- Well, I'm not sure what exactly "negligibly small" means. So far I get the impression that a one-way function is something like "a computable and deterministic function such that, given an output, an input that would result in the output cannot be found in a reasonable amount of time". But what's reasonable? —Simetrical (talk • contribs) 04:46, 19 February 2006 (UTC)
I find the way we usually denote this in class more readable:
2. hard to invert
Although more wordy, I think it's much clearer broken up into steps like this.
Meekohi 16:58, 1 January 2006 (UTC)
- Erm . . . okay. You cryptographers can talk about that, and I'll just step to the side. Only, it doesn't really belong in a section about definitions being comprehensible to laymen. :) —Simetrical (talk • contribs) 11:02, 3 January 2006 (UTC)
I agree. I studied a lot of mathematics courses at university level, and I can't seem to understand the definition. I'd like a little bit more clarification. What does the * mean? Is {0, 1} a set, and interval or something else? What does it mean to be "sufficently large"? Is there a formal definition of this? Does it mean the limit of some expression goes to zero when n goes to infinity? Maybe if we don't explain it in text we should at least have a few clickable links to other articles for further clarification. I really didn't understand the definition and feel it should be possible to explain it in an alterative way. — Preceding unsigned comment added by 78.72.135.178 (talk) 09:32, 20 November 2017 (UTC)
The formal definition is incomplete
[edit]The formal definition of "strong one-way function" is incomplete, because it refers to a "probabilistic polynomial-time algorithm" A' without defining what this is, so that when A' gets used in the expression
it's not clear what's going on. I tried to partially cure this by adding a link to "random algorithm" (since this is where a query about "probabilistic algorithm" got redirected). Alas, it's not a complete cure, since that article does not give a formal definition of probabilistic algorithm.
Since I've studied this subject a wee bit, I can guess that a probabilistic algorithm takes two inputs: the "actual" input and also an auxiliary random string. So, I can guess that these are the two arguments of A' above. But the discussion after the definition seems to be saying that the role of is just to tell A' the length of the string it's trying to compute. So maybe the auxiliary random string is completely implicit in the above expression??
A clear definition of "probabilistic algorithm", or a link to one, would not have made me guess so much.
The worst thing is, I really need to know the definition TODAY! :-)
John Baez 09:47, 10 February 2006 (UTC)
- See Probabilistic Turing machine. Could be better named. Deco 11:59, 10 February 2006 (UTC)
- The auxiliary string isn't so much to inform the algorithm, it's simply to enforce a minimum length on the input. This is important because we defined the algorithm as working in polynomial time (implicitly tied to input length), but we actually just want the full f∘A'∘f to work in polynomial time, and the size of the input to f can dominate the size of the input to A'. I've removed the auxiliary string from the definition and added language instead, to reduce confusion. 88.115.207.64 (talk) 17:48, 29 October 2015 (UTC)
Other types of function
[edit]This article needs an early explanation about whether it is the same as a trapdoor function or not, and whether it can in theory be inverted at all (i.e. whether it is an injective function) - the hash function function suggests no, but this article seems to suggest yes. --Henrygb 23:07, 6 March 2006 (UTC)
Question...
[edit]I'm not sure if it's appropriate to ask a question like this on a wikipedia talk page (rather than a discussion forum), but: If I understand correctly, f^-1(f(x)) = x for all x. If, for example, we have f(x) = x mod 5, surely there's no possible f^-1? f(5), f(10), f(15) etc. all = 0, so how can it be possible to construct an inverse function that can correctly return either of these original values for the input 0? In other words: what's the difference between a one-way function and a non one-to-one function? I assume that there must in fact be some difference, because of the assertion in the article that mathematicians aren't sure whether true one-way functions exist (so either I'm wrong about what one-way functions are, the article is wrong about what mathematicians think, or I've somehow made a groundbreaking discovery (ha, ha)). - SoulSkorpion 08:05, 11 June 2006 (UTC)
- You're reading too much into the definition. g(f(x))=x only says that g is a left inverse of f (not a total inverse since f may not be 1-to-1). That is, given y it returns some value z such that y=f(z). If f maps two values to y, g should return one of these two values, but we don't care which. In your example, the identity function g(x)=x is a left inverse of f(x)=x%5 Blokhead 13:50, 12 June 2006 (UTC)
- Bah, I should check the definitions before I post... anyway, the idea is the same, but notice how f^{-1}(f(x)) is used as a set of values in the definitions, not a single-valued thing. f^{-1}(y) is the set of all x's that f maps to y. Again, the algorithm could return any one of these, we don't care which. Forget what I said about left inverses.. Blokhead 13:54, 12 June 2006 (UTC)
- To say that "surely there's no possible f^-1" is where you went wrong. No one ever said that f was invertable, more precicely no one ever said that f had to be injective. The classes of injective and one-way functions are distinct; for a one-way function it is computationally hard to find a preimage, for a injective function preimages are unique. 129.94.6.30 00:04, 18 September 2006 (UTC)
Choice of factoring algorithm?
[edit]I'm a bit perplexed why the asymptotic time cited here is for elliptic curve factoring, rather than the number field sieve. Generally the sort of worst-case numbers used in cryptography are most efficiently factored with NFS, right? Deco 20:07, 11 June 2006 (UTC)
There is a mistake in the prime multiplication section, the complexity of the factorization algorithm is given as O(2(log N)1/3(log log N)2/3), but log log N < log N, so 2(log N)1/3(log log N)2/3 < 2log N = Nlog 2 < N2, therefore O(2(log N)1/3(log log N)2/3) is a subset of O(N2). Either O(2(log N)1/3(log log N)2/3) is not the complexity of the factorization algorithm or else prime multiplication is not a one-way function. Wolfram[1] gives prime multiplication as an example of a potential one-way function so I suspect that the factorization complexity is incorrect. Also, the integer factorization page gives the complexity as O(exp((64/9 N)1/3(log N)2/3)) = O(2N1/3(log N)2/3). Daspiffy 23:26, 30 January 2013 (UTC).
References
- ^ "One-Way Function". Wolfram.
Plagiarized
[edit]The definitions on this page of strong and weak one-way functions (and most of the text surrounding them) were clearly plagiarized (with minor modifications) from Oded Goldreich's book Foundations of Cryptography I (see pp.33-35). Please remove them. --- Tom Roeder, Cornell University
I've removed the text for now. I presume it is a near word-for-word copying, and not just a re-expression of the same definition? (I don't have access to Goldreich's book). — Matt Crypto 17:03, 15 September 2006 (UTC)
- A link to Goldreichs book is given at the end of the article. The definitions of strong and weak one-way functions go back to at least 1982 (e.g. an paper by Yao includes them). So the definitions can safely be inserted in the article again. Thus it seems that only the additional explanations between the definitions need to be discussed. There is nothing new there either. Just some well written text. Maybe the explanations can be left away or rewritten. I wouldn't even call the old version plagiarism, rather a case of fair use. 67.84.116.166 01:04, 17 September 2006 (UTC)
See http://www.wisdom.weizmann.ac.il/~oded/foc-drafts.html for drafts of the book that contain the defs and some of the same text. Looking at the final copy in the book, however, shows that the copying was almost word-for-word. I don't have Yao's paper in front of me, but I agree that his definition (or any other) could be used, if it is cited properly. --- Tom Roeder
False statement?
[edit]The article states that "One-way functions exist implies P NP, but it's not clear if P NP implies the existence of one way function." However the other direction has already been proved. See Chapter 2 of The Complexity Theory Companion. -- Pku_leehsin
- Don't have that book, but if your book says "PNP implies one way functions", then it's certainly talking about complexity (worst-case) one way functions, not cryptographic (average-case) one-way functions. It can get confusing, but no one really does anything with worst-case OWFs these days. Blokhead 03:09, 30 October 2006 (UTC)
I am quite certain that having a constructive proof of P=NP would bring you no closer to reversing SHA-1 or SHA-256. --- Joshua
- Reading the pseudocode for SHA-256, I can tell you with absolute confidence that it would. In fact, if that code is accurate, I could write a program right now that could decrypt it in time polynomial in the length of the data and the computation time of kSAT's implementation, and I don't think I'd even need to open a book. Twin Bird (talk) 07:28, 18 June 2011 (UTC)
List_of_open_problems_in_computer_science#The_existence_of_one-way_functions says that P NP does not imply the existence of a one-way function. This contradicts what is said in this article. 192.87.139.139 (talk) 12:16, 24 May 2011 (UTC)
- Where? It says "Existence of a proof that P and NP are not equal would not imply the existence of one-way functions" right in the article as it stands. It contradicts Pku_leehsin, but not the article. Are you confusing the assertion with its converse? Because a proof that one-way functions exist would imply P NP, and a proof that P = NP (which is about as likely as the Riemann hypothesis being false) would imply their nonexistence. However, a proof that P NP would not imply the existence of one-way functions, nor would their nonexistence imply P = NP. Twin Bird (talk) 05:32, 18 June 2011 (UTC)
One-Time Pad?
[edit]This article says that the existence of a one-way function implies the existence of a private-key encryption scheme. Isn't this trivially true, due to the existence of the one-time pad? 71.194.163.223 13:50, 24 July 2007 (UTC)
- I have clarified this in the article. OWF implies private-key encryption that is secure against chosen-plaintext and chosen-ciphertext attacks. One-time pad certainly doesn't meet this, as you need a fresh key for each new message sent. Blokhead 14:53, 24 July 2007 (UTC)
Worst case vs average case
[edit]- Note that, by this definition, the function must be "hard to invert" in the average-case, rather than worst-case sense; while in most of complexity theory (e.g., NP-hardness) the term "hard" is meant in the worst-case.
This is just confusing concepts.
"Average case", as in taking mean time across all valid inputs, as in ZPP class, is not what we want. We want something much stronger - we want inverting to be hard for overwhelming majority of cases.
For example, if we had a function f(x) which always took 4^(number of bits in x) time (under P!=NP and whatever other assumptions we need), then the function g(x) = 2*f(x) if x prime, g(x) = 2*x+1 otherwise, would still take exponential time on average to reverse (sum 4^log2(x)/ln(x)/N = sum x^2/ln(x)/N \in O(x)), but vast majority of cases would be trivially invertible, making such function useless as a one-way function. Taw (talk) 11:02, 16 September 2009 (UTC)
Universal one-way function section makes almost no sense
[edit]It's very hard to understand... I get the general sense from this section that there exists a function that if proved to be one way, would prove that functions can be one way. But it doesn't explain much else... — Preceding unsigned comment added by 69.117.26.39 (talk) 00:33, 20 February 2013 (UTC)
- I have edited the section to clarify its meaning, which is that there exists a function f such that if any function is one-way, then so is f. --Joshua Issac (talk) 13:04, 29 August 2013 (UTC)
- Still is probably the vaguest statement I have ever read on wikipedia. 128.54.162.174 (talk) 07:29, 11 December 2013 (UTC)
One way function proven:
[edit]Here is a one-way function that is impossible to derive its input based on outputs: f(x)=0. What is this article or definition missing? Average64 (talk) 19:51, 27 May 2014 (UTC)
- This example is discussed in the section "Theoretical definition". f(x)=0 is not a one-way function. Hence nothing is missing here. 92.106.209.242 (talk) 11:10, 29 May 2014 (UTC)
Wrong integer multiplication upper bound
[edit]AFAIK, it's not O(n^2) as stated in the article. See Fürer's algorithm, it can reach O(n\log n2^{3\log^* n}) Willrazen (talk) 19:27, 2 February 2016 (UTC)
Explanation/Mention of Common Imprecise Usage of "One-Way Function"
[edit]I think it'd be a good idea to add one sentence to the header explaining that people often use the term "one-way function" to apply to functions that, while currently difficult to invert, may or may not be one-way functions under the formal definition of the term. (In fact, the articles for hash functions and cryptographic hash functions both describe them as being one-way functions.) There already is the section on "Candidates for one-way functions" but it's much further down and common alternate (albeit imprecise) usages of the term probably warrants some mention in the header. Thoughts? Jwuthe2 (talk) 11:45, 2 November 2017 (UTC)
Rabin function is "trapdoor" not "one way"
[edit]The "Rabin function" (squaring modulo some two-factor integer N) is one-way only if the factorization of N is not known. For any such N, that function is easy to invert. Thus it is not a "one-way function" but rather a "trapdoor function" (when N is included as the parameter of f and p,q as parameters of the inverse). It should be removed and discussed only in the trapdoor function article. --Jorge Stolfi (talk) 21:33, 15 August 2018 (UTC)
Existence of one-way functions and implications to P and NP
[edit]On the one hand, the article states "[...] their existence would prove that the complexity classes P and NP are not equal [..]", but on the other hand also in an other section "The existence of one-way functions also implies that there is no natural proof for P≠NP". Are both implications true? If yes, what is the point of ever presenting the second one without the first one? — Preceding unsigned comment added by 2A02:8070:8798:4000:80E4:FDE0:A138:9EB6 (talk) 22:46, 7 February 2020 (UTC)
- I have removed the latter ("The existence of one-way functions also implies that there is no natural proof for P≠NP") because it is ambiguous. The existence of OWF implies that P≠NP directly which is stronger than saying no natural proof exists (the statement is relying on the fact that OWF implies the existence of PRF which in turn implies that no natural proof exists). PolyCreator (talk) 02:12, 10 April 2022 (UTC)
Generalization
[edit]As defined here, one-way functions are defined so they are polynomial time, but their inverse is not. However, the same concept could be thought of more generally as functions with a strict upper bound that is a lower bound on their inverse. Is there any information about this more general problem, how it is formulated and described, it’s implications, and whether or not it has been solved?
Half probability that prime is even?
[edit]In the section Candidates for one way functions, it is stated "...because the probability that an arbitrary p is odd is 1/2, and likewise for q(...)". But since 2 is the only even prime, that seems not correct? 89.99.34.48 (talk) 07:11, 24 July 2022 (UTC)
"However, P≠NP does not imply the existence of one-way functions."
[edit]This statement implies P != NP and is therefore currently unknown. It should therefore be removed. (If P = NP, then P != NP is false and thus trivially implies anything.) --fiesh 91.43.222.42 (talk) 23:21, 15 November 2022 (UTC)
Editor's note
[edit]I was reading the page, and in consulting the sources for the page noticed that the source for "Lecture Notes on Cryptography" is outdated. I don't have anything else to contribute just wanted to inform the lovely editors of this page. Zipore (talk) 19:27, 6 January 2025 (UTC)

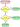




![{\displaystyle Pr[x\leftarrow \{0,1\}^{k};y\leftarrow f(x);x'\leftarrow A(y,1^{k}):f(x')=f(x)]\leq {\frac {1}{2^{k}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/390a035890d327425935e1f250face35fee1d7ba)


