Cylindrical polar coordinates Source: en.wikipedia.org/wiki/Cylindrical_polar_coordinates

A cylindrical coordinate system is a three-dimensional coordinate system that specifies point positions around a main axis (a chosen directed line) and an auxiliary axis (a reference ray). The three cylindrical coordinates are: the point perpendicular distance ρ from the main axis; the point signed distance z along the main axis from a chosen origin; and the plane angle φ of the point projection on a reference plane (passing through the origin and perpendicular to the main axis)

The main axis is variously called the cylindrical or longitudinal axis. The auxiliary axis is called the polar axis, which lies in the reference plane, starting at the origin, and pointing in the reference direction. Other directions perpendicular to the longitudinal axis are called radial lines.

The distance from the axis may be called the radial distance or radius, while the angular coordinate is sometimes referred to as the angular position or as the azimuth. The radius and the azimuth are together called the polar coordinates, as they correspond to a two-dimensional polar coordinate system in the plane through the point, parallel to the reference plane. The third coordinate may be called the height or altitude (if the reference plane is considered horizontal), longitudinal position,^[1] or axial position.^[2]

Cylindrical coordinates are useful in connection with objects and phenomena that have some rotational symmetry about the longitudinal axis, such as water flow in a straight pipe with round cross-section, heat distribution in a metal cylinder, electromagnetic fields produced by an electric current in a long, straight wire, accretion disks in astronomy, and so on.

They are sometimes called cylindrical polar coordinates^[3] or polar cylindrical coordinates,^[4] and are sometimes used to specify the position of stars in a galaxy (galactocentric cylindrical polar coordinates).^[5]

The three coordinates (ρ, φ, z) of a point P are defined as:

• The radial distance ρ is the Euclidean distance from the z-axis to the point P.
• The azimuth φ is the angle between the reference direction on the chosen plane and the line from the origin to the projection of P on the plane.
• The axial coordinate or height z is the signed distance from the chosen plane to the point P.

As in polar coordinates, the same point with cylindrical coordinates (ρ, φ, z) has infinitely many equivalent coordinates, namely (ρ, φ ± n×360°, z) and (−ρ, φ ± (2n + 1)×180°, z), where n is any integer. Moreover, if the radius ρ is zero, the azimuth is arbitrary.

In situations where someone wants a unique set of coordinates for each point, one may restrict the radius to be non-negative (ρ ≥ 0) and the azimuth φ to lie in a specific interval spanning 360°, such as [−180°,+180°] or [0,360°].

The notation for cylindrical coordinates is not uniform. The ISO standard 31-11 recommends (ρ, φ, z), where ρ is the radial coordinate, φ the azimuth, and z the height. However, the radius is also often denoted r or s, the azimuth by θ or t, and the third coordinate by h or (if the cylindrical axis is considered horizontal) x, or any context-specific letter.

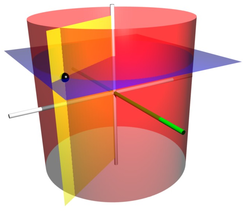
In concrete situations, and in many mathematical illustrations, a positive angular coordinate is measured counterclockwise as seen from any point with positive height.

The cylindrical coordinate system is one of many three-dimensional coordinate systems. The following formulae may be used to convert between them.

For the conversion between cylindrical and Cartesian coordinates, it is convenient to assume that the reference plane of the former is the Cartesian xy-plane (with equation z = 0), and the cylindrical axis is the Cartesian z-axis. Then the z-coordinate is the same in both systems, and the correspondence between cylindrical (ρ, φ, z) and Cartesian (x, y, z) are the same as for polar coordinates, namely $${\displaystyle {\begin{aligned}x&=\rho \cos \varphi \\y&=\rho \sin \varphi \\z&=z\end{aligned}}}$$ in one direction, and $${\displaystyle {\begin{aligned}\rho &={\sqrt {x^{2}+y^{2}}}\\\varphi &={\begin{cases}{\text{indeterminate}}&{\text{if }}x=0{\text{ and }}y=0\\\arcsin \left({\frac {y}{\rho }}\right)&{\text{if }}x\geq 0\\-\arcsin \left({\frac {y}{\rho }}\right)+\pi &{\mbox{if }}x<0{\text{ and }}y\geq 0\\-\arcsin \left({\frac {y}{\rho }}\right)-\pi &{\mbox{if }}x<0{\text{ and }}y<0\end{cases}}\end{aligned}}}$$ in the other. The arcsine function is the inverse of the sine function, and is assumed to return an angle in the range [−⁠π/2⁠, +⁠π/2⁠] = [−90°, +90°]. These formulas yield an azimuth φ in the range [−180°, +180°].

By using the arctangent function that returns also an angle in the range [−⁠π/2⁠, +⁠π/2⁠] = [−90°, +90°], one may also compute ${\displaystyle \varphi }$ without computing ${\displaystyle \rho }$ first $${\displaystyle {\begin{aligned}\varphi &={\begin{cases}{\text{indeterminate}}&{\text{if }}x=0{\text{ and }}y=0\\{\frac {\pi }{2}}{\frac {y}{|y|}}&{\text{if }}x=0{\text{ and }}y\neq 0\\\arctan \left({\frac {y}{x}}\right)&{\mbox{if }}x>0\\\arctan \left({\frac {y}{x}}\right)+\pi &{\mbox{if }}x<0{\text{ and }}y\geq 0\\\arctan \left({\frac {y}{x}}\right)-\pi &{\mbox{if }}x<0{\text{ and }}y<0\end{cases}}\end{aligned}}}$$ For other formulas, see the article Polar coordinate system.

Many modern programming languages provide a function that will compute the correct azimuth φ, in the range (−π, π), given x and y, without the need to perform a case analysis as above. For example, this function is called by atan2(y, x) in the C programming language, and (atan y x) in Common Lisp.

Spherical coordinates (radius r, elevation or inclination θ, azimuth φ), may be converted to or from cylindrical coordinates, depending on whether θ represents elevation or inclination, by the following:

Conversion between spherical and cylindrical coordinates

Conversion to:	Coordinate	θ is elevation	θ is inclination
Cylindrical	ρ =	r cos θ	r sin θ
	φ =	φ
	z =	r sin θ	r cos θ
Spherical	r =	${\textstyle {\sqrt {\rho ^{2}+z^{2}}}}$
	θ =	${\textstyle \arctan \left({\frac {z}{\rho }}\right)}$	${\textstyle \arctan \left({\frac {\rho }{z}}\right)}$
	φ =	φ

In many problems involving cylindrical polar coordinates, it is useful to know the line and volume elements; these are used in integration to solve problems involving paths and volumes.

The line element is $${\displaystyle \mathrm {d} {\boldsymbol {r}}=\mathrm {d} \rho \,{\boldsymbol {\hat {\rho }}}+\rho \,\mathrm {d} \varphi \,{\boldsymbol {\hat {\varphi }}}+\mathrm {d} z\,{\boldsymbol {\hat {z}}}.}$$

The volume element is $${\displaystyle \mathrm {d} V=\rho \,\mathrm {d} \rho \,\mathrm {d} \varphi \,\mathrm {d} z.}$$

The surface element in a surface of constant radius ρ (a vertical cylinder) is $${\displaystyle \mathrm {d} S_{\rho }=\rho \,\mathrm {d} \varphi \,\mathrm {d} z.}$$

The surface element in a surface of constant azimuth φ (a vertical half-plane) is $${\displaystyle \mathrm {d} S_{\varphi }=\mathrm {d} \rho \,\mathrm {d} z.}$$

The surface element in a surface of constant height z (a horizontal plane) is $${\displaystyle \mathrm {d} S_{z}=\rho \,\mathrm {d} \rho \,\mathrm {d} \varphi .}$$

The del operator in this system leads to the following expressions for gradient, divergence, curl and Laplacian: $${\displaystyle {\begin{aligned}\nabla f&={\frac {\partial f}{\partial \rho }}{\boldsymbol {\hat {\rho }}}+{\frac {1}{\rho }}{\frac {\partial f}{\partial \varphi }}{\boldsymbol {\hat {\varphi }}}+{\frac {\partial f}{\partial z}}{\boldsymbol {\hat {z}}}\\[8px]\nabla \cdot {\boldsymbol {A}}&={\frac {1}{\rho }}{\frac {\partial }{\partial \rho }}\left(\rho A_{\rho }\right)+{\frac {1}{\rho }}{\frac {\partial A_{\varphi }}{\partial \varphi }}+{\frac {\partial A_{z}}{\partial z}}\\[8px]\nabla \times {\boldsymbol {A}}&=\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \varphi }}-{\frac {\partial A_{\varphi }}{\partial z}}\right){\boldsymbol {\hat {\rho }}}+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right){\boldsymbol {\hat {\varphi }}}+{\frac {1}{\rho }}\left({\frac {\partial }{\partial \rho }}\left(\rho A_{\varphi }\right)-{\frac {\partial A_{\rho }}{\partial \varphi }}\right){\boldsymbol {\hat {z}}}\\[8px]\nabla ^{2}f&={\frac {1}{\rho }}{\frac {\partial }{\partial \rho }}\left(\rho {\frac {\partial f}{\partial \rho }}\right)+{\frac {1}{\rho ^{2}}}{\frac {\partial ^{2}f}{\partial \varphi ^{2}}}+{\frac {\partial ^{2}f}{\partial z^{2}}}\end{aligned}}}$$

The solutions to the Laplace equation in a system with cylindrical symmetry are called cylindrical harmonics.

In a cylindrical coordinate system, the position of a particle can be written as^[6] $${\displaystyle {\boldsymbol {r}}=\rho \,{\boldsymbol {\hat {\rho }}}+z\,{\boldsymbol {\hat {z}}}.}$$ The velocity of the particle is the time derivative of its position, $${\displaystyle {\boldsymbol {v}}={\frac {\mathrm {d} {\boldsymbol {r}}}{\mathrm {d} t}}={\dot {\rho }}\,{\boldsymbol {\hat {\rho }}}+\rho \,{\dot {\varphi }}\,{\hat {\boldsymbol {\varphi }}}+{\dot {z}}\,{\hat {\boldsymbol {z}}},}$$ where the term ${\displaystyle \rho {\dot {\varphi }}{\hat {\varphi }}}$ comes from the Poisson formula ${\displaystyle {\frac {\mathrm {d} {\hat {\rho }}}{\mathrm {d} t}}={\dot {\varphi }}{\hat {z}}\times {\hat {\rho }}}$. Its acceleration is^[6] $${\displaystyle {\boldsymbol {a}}={\frac {\mathrm {d} {\boldsymbol {v}}}{\mathrm {d} t}}=\left({\ddot {\rho }}-\rho \,{\dot {\varphi }}^{2}\right){\boldsymbol {\hat {\rho }}}+\left(2{\dot {\rho }}\,{\dot {\varphi }}+\rho \,{\ddot {\varphi }}\right){\hat {\boldsymbol {\varphi }}}+{\ddot {z}}\,{\hat {\boldsymbol {z}}}}$$

• List of canonical coordinate transformations
• Vector fields in cylindrical and spherical coordinates
• Del in cylindrical and spherical coordinates

• Morse, Philip M.; Feshbach, Herman (1953). Methods of Theoretical Physics, Part I. New York City: McGraw-Hill. pp. 656–657. ISBN 0-07-043316-X. LCCN 52011515. {{cite book}}: ISBN / Date incompatibility (help)
• Margenau, Henry; Murphy, George M. (1956). The Mathematics of Physics and Chemistry. New York City: D. van Nostrand. p. 178. ISBN 9780882754239. LCCN 55010911. OCLC 3017486. {{cite book}}: ISBN / Date incompatibility (help)
• Korn, Granino A.; Korn, Theresa M. (1961). Mathematical Handbook for Scientists and Engineers. New York City: McGraw-Hill. pp. 174–175. LCCN 59014456. ASIN B0000CKZX7.
• Sauer, Robert; Szabó, István (1967). Mathematische Hilfsmittel des Ingenieurs. New York City: Springer-Verlag. p. 95. LCCN 67025285.
• Zwillinger, Daniel (1992). Handbook of Integration. Boston: Jones and Bartlett Publishers. p. 113. ISBN 0-86720-293-9. OCLC 25710023.
• Moon, P.; Spencer, D. E. (1988). "Circular-Cylinder Coordinates (r, ψ, z)". Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed.). New York City: Springer-Verlag. pp. 12–17, Table 1.02. ISBN 978-0-387-18430-2.

• "Cylinder coordinates", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• MathWorld description of cylindrical coordinates
• Cylindrical Coordinates Animations illustrating cylindrical coordinates by Frank Wattenberg